The concept of De Broglie wavelength is fundamental in quantum mechanics and plays a crucial role in understanding the dual nature of matter. This article will explore the intricacies of De Broglie wavelength, its significance in physics, and its applications in various fields. By the end, you'll have a clear understanding of what De Broglie wavelength is and why it matters.
The notion that particles can exhibit wave-like behavior was introduced by the French physicist Louis de Broglie in 1924. This revolutionary idea marked a significant shift in physics, leading to the development of wave-particle duality, which has profound implications for the study of quantum mechanics. The De Broglie wavelength provides a way to calculate the wavelength associated with a moving particle, bridging the gap between classical and quantum physics.
In this article, we will delve into the formula for De Broglie wavelength, its derivation, and its applications in various scientific domains. Additionally, we will analyze the implications of this theory and how it has influenced modern physics. So, whether you are a student, a researcher, or simply curious about the subject, this guide is designed to enhance your understanding of De Broglie wavelength.
Table of Contents
- What is De Broglie Wavelength?
- The Formula of De Broglie Wavelength
- Derivation of the De Broglie Wavelength
- Significance of De Broglie Wavelength
- Applications of De Broglie Wavelength
- De Broglie Wavelength in Quantum Mechanics
- Experiments Confirming De Broglie Wavelength
- Conclusion
What is De Broglie Wavelength?
The De Broglie wavelength is the wavelength associated with a moving particle and is a key concept in quantum mechanics. According to de Broglie’s hypothesis, every moving particle or object has an associated wave. This means that particles such as electrons, protons, and even larger objects can exhibit wave-like behavior under certain conditions.
The De Broglie wavelength is calculated using the formula:
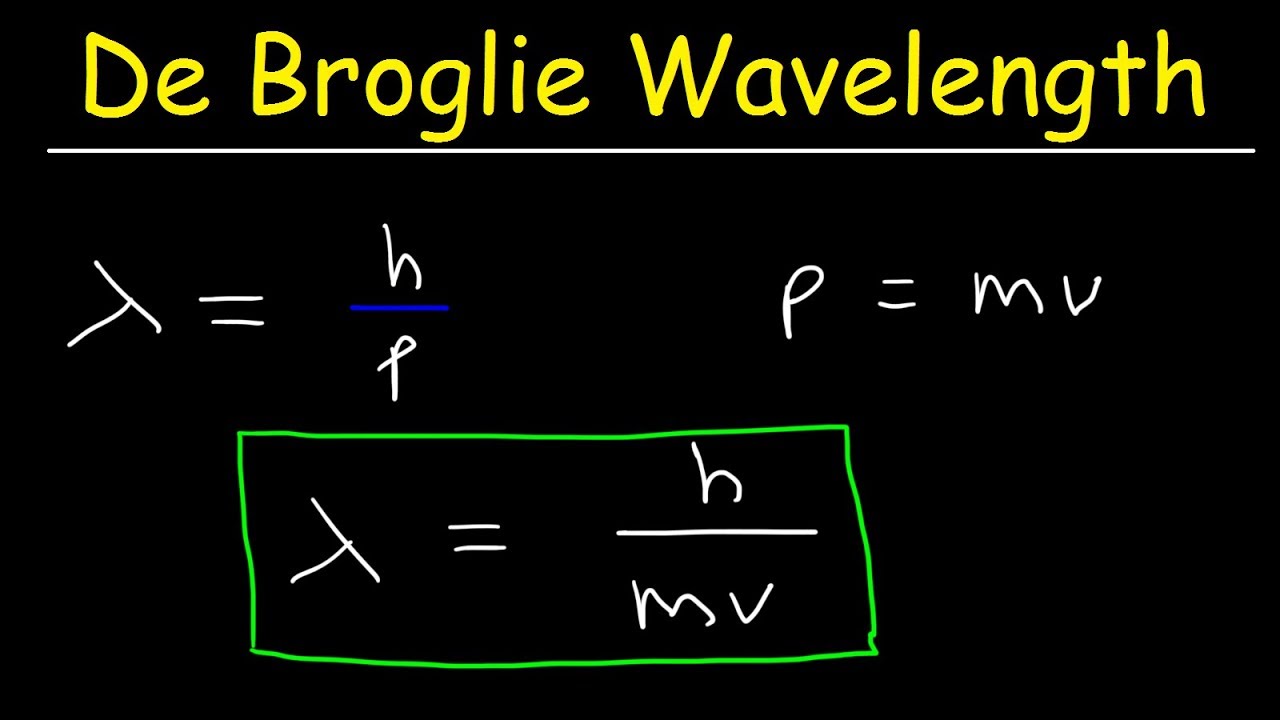
λ = h / p
Where:
- λ (lambda) is the De Broglie wavelength.
- h is the Planck constant (6.62607015 × 10^-34 m² kg / s).
- p is the momentum of the particle (mass × velocity).
The Formula of De Broglie Wavelength
The formula for De Broglie wavelength can be expressed as:
λ = h / mv
Where:
- m = mass of the particle.
- v = velocity of the particle.
This formula shows the inverse relationship between the particle's momentum and its wavelength—higher momentum results in a shorter wavelength, while lower momentum leads to a longer wavelength.
Derivation of the De Broglie Wavelength
The derivation of the De Broglie wavelength can be approached through the principles of wave-particle duality and the energy-momentum relationship. De Broglie used the idea that energy can be expressed in terms of frequency and wavelength.
1. The energy of a photon is given by:
E = hf
2. The momentum of a photon is given by:
p = E/c
3. By substituting the first equation into the second, we get:
p = hf/c
4. For matter waves, de Broglie postulated that particles also have momentum, leading to the formulation:
λ = h / p
Through this derivation, de Broglie established a connection between classical mechanics and quantum mechanics.
Significance of De Broglie Wavelength
The significance of De Broglie wavelength lies in its implications for the nature of matter and energy. It provides a framework to understand the behavior of particles at the quantum level and has led to several groundbreaking developments in physics.
- **Wave-Particle Duality**: The concept challenges the classical notion that particles and waves are distinct entities.
- **Quantum Mechanics**: De Broglie’s hypothesis was pivotal in the development of quantum mechanics and the Schrödinger equation, which describes how quantum states evolve over time.
- **Electron Microscopy**: The application of De Broglie wavelength concepts has allowed scientists to develop electron microscopes that can resolve structures at the atomic level.
Applications of De Broglie Wavelength
The concept of De Broglie wavelength finds applications across various fields of science and technology:
- **Quantum Computing**: The principles of quantum mechanics, including De Broglie wavelength, are foundational in the development of quantum computers.
- **Nanotechnology**: Understanding the wave nature of particles is essential in manipulating materials at the nanoscale.
- **Spectroscopy**: De Broglie wavelength is used in spectroscopy techniques to analyze the properties of materials.
De Broglie Wavelength in Quantum Mechanics
In quantum mechanics, the De Broglie wavelength is essential for describing the behavior of particles in potential wells and barriers. The wave-like properties of particles lead to phenomena such as quantum tunneling, where particles can pass through energy barriers that they classically should not be able to cross.
Additionally, the concept of wave functions, which describe the probability distribution of a particle's position, is deeply rooted in the ideas introduced by De Broglie.
Experiments Confirming De Broglie Wavelength
Several experiments have confirmed the existence of De Broglie wavelengths in particles:
- **Electron Diffraction**: Experiments with electron beams passing through thin films show interference patterns, confirming their wave-like behavior.
- **Double-Slit Experiment**: This classic experiment demonstrates wave-particle duality, showing that particles can exhibit interference patterns.
These experiments validate the predictions made by De Broglie's theory and highlight the fundamental principles of quantum mechanics.
Conclusion
In conclusion, the De Broglie wavelength is a cornerstone of modern physics, bridging the gap between classical and quantum mechanics. Understanding this concept is essential for grasping the behavior of matter at the quantum level. From its formulation to its applications in various fields, the De Broglie wavelength continues to inspire scientific inquiry and technological advancements.
We encourage you to explore further on this topic, engage in discussions, and share your insights on De Broglie wavelength. Feel free to leave your comments below and share this article with others interested in the fascinating world of quantum physics.
Thank you for reading! We hope to see you back here for more insightful articles on science and technology.